天文学中的数值模拟:编外篇之四·N体模拟的可靠性
众所周知,N体问题中只有N=2时才存在精确的解析解,而其他情况只能给出数值解,只有限制性三体问题等极少数例外。N体模拟的目的就是用数值方法来求算大量天体之间的引力相互作用。但是这里的一个严重问题是,数值方法不可避免地会引入误差,而N体问题很多都属于混沌系统,初始的微小扰动会导致随后演化出现很大的偏差,因此N体模拟给出的结果是否能够准确地反映系统的真实情况?圈内对此的默认回答是,虽然单次模拟未必真实,但多次模拟结果的统计性质应该与实际相去不远。不过这个回答只是假设而已,而最近读到的Boekholt & Portegies Zwart (2014)就是希望通过实际计算来证实或证伪这一条假设。
为了达到这一目的,两位作者专门开发了一组N体模拟代码Brutus。这里的关键是要控制好计算过程中的误差来源,这其中包括数值积分过程中必需的离散化导致的偏差以及计算机的截断误差。第一点的控制方法是Bulirsch-Stoer方法,它可以通过比较各次迭代的收敛性,将数值积分误差控制到所需的范围之内;第二点则可以通过定义任意精度的变量,增加有效位数的方法来减小。另外还有初始条件的不确定性,不过如果初条只是遵循特定的统计分布,这倒也不是太大的问题。比较Brutus计算精度的基准是引力模拟最流行的四阶Hermite算法。为探讨不同精度下模拟结果收敛性的问题,作者又引入了两个解之间的相空间距离δ,若δ在整个模拟期间都不大于某个小量(如千分之一),则可以认为解是收敛的。
在考察N体模拟可靠性问题之前,作者先使用Brutus,在不同精度下对若干经典问题进行了测试。首先是Pythagorean三体问题,根据先前的研究,这一系统在经历若干三体的近距离遭遇后,最终会演化为二体问题+逃逸天体的组合。不过文中引用的相关文献居然不是英文的,本人没有去考察这个问题的细节。Brutus的运行速度慢于Hermite算法,结果也与后者不尽相同。Hermite算法可以精确再现逃逸天体出现之前的过程,但之后由于最终一次三体密近遭遇引入的能量误差,δ增至1以上,而且减小积分步长也不能很好地降低δ,因此与Brutus的模拟结果出现了较大偏差。作为比较,只要数值积分的误差控制得足够小,Brutus对于δ的控制要好上很多,自始至终δ都保持相对稳定,因此可以获得可靠的收敛解。
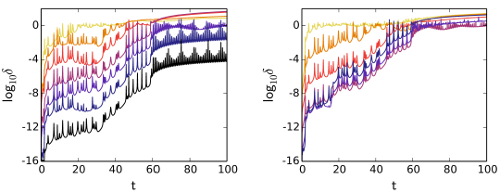
Brutus(左)与Hermite(右)算法计算Pythagorean三体问题时的收敛性比较。左图描绘了Brutus计算的结果在整个模拟过程中的δ演化,从上到下依次代表数值积分误差容忍度各取10-2与10-4、10-4与10-6、10-6与10-8、10-8与10-10、10-10与10-12、10-12与10-14、10-14与10-16时两解之间的δ。右图是Hermite算法时间步长参数各取2-3、2-5、2-7、2-9、2-11、2-13时的δ演化。可见只要积分精度足够好,Brutus可以很好地控制δ,但Hermite算法在这一点的表现要差很多。(图片来源:Boekholt & Portegies Zwart 2014)
随后作者还测试了等边三角形构型的三体问题和16体Plummer问题,也就是星团中双星的动力学形成过程。在这两个问题中,无论使用哪种算法求解,最终的结果都出现了发散,这说明某些问题最终出现的发散是源自物理的,而非计算精度。
这样就进入了正式的考察过程。出于节约计算时间的考虑,对N体模拟可靠性的考察是以4种三体问题作为样本的。它们都以Plummer分布为基础,只是初始质量比以及速度分布有所不同,分别是三体质量相同、质量比1:2:4、质量相同且初始速度为0(所谓的“冷”系统)、质量比1:2:4且初始速度为0,位置以及前两种情况下的速度则根据位力化的Plummer分布来随机选择,一共用两种算法各模拟了一万组。当三体系统演化成为一对双星外加一个逃逸天体时,相应的模拟即告终止。

Brutus模拟出的三体系统参数分布与解析解的比较,图中黑色曲线表示解析分布,4种形状的数据点对应4种三体系统构型的模拟结果。左上:逃逸天体的速度;右上:逃逸天体的动能;左下:双星系统的偏心率;右下:双星系统的束缚能量。(图片来源:Boekholt & Portegies Zwart 2014)
首先要说的是,Brutus模拟出的三体系统各参数分布与解析结果很相似。由于前述对δ的控制能力优良,且数值结果与解析解接近,Brutus得出的结果可以认为是可靠的真实解。要问不可解析求解的三体问题哪里又有什么参数的解析分布?这一点的得出说来也不难,是根据相应系统构型占据的相空间体积比例来估算的。Brutus与Hermite所得结果之间的相似性是利用统计学上常用的Kolmogorov-Smirnov检验来讨论的。只要时间步长参数足够小,两种算法并无显著差异。但由于时间步长过大时Hermite算法不再完全满足能量守恒条件,差异开始出现了。这样看来,为得到可靠的结果,足够密的时间格点是必须的。当然,从数值积分的原理上看,这一点也并不难理解,其实在实际操作中,只要硬件条件允许,总计算时间尚可容忍,研究者也都会尽量缩小步长的。
两种算法单次模拟结果的比较就是另一回事了。只有当模拟时间足够小的时候,二者就某组特定参数和初始条件得出的结果才会足够相似。无论时间步长取得多么小,最终也只有四到七成的结果能够做到彼此一致,可以认为是精确解。这是因为当时间步长缩小到一定程度之后,虽然解域离散化误差减少,但总的积分步骤增加,在精度不变的前提下,累积起来的舍入误差也随之上涨,总误差不会存在太大变化。
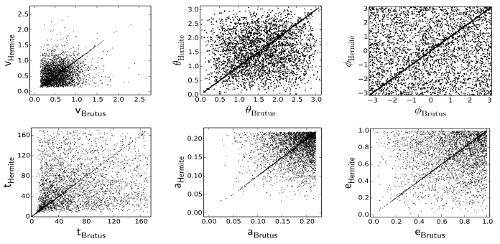
Brutus(X轴)与Hermite(Y轴)各次模拟结果比较的散点图。图中各图贯穿对角线的斜线表示二者相等的精确解,只有当两种算法给出的解在相空间中的距离小于十分之一时,相应的点才能落到对角线上,否则会散布在其余各处。左上:逃逸天体的速度;中上与右上:逃逸天体运动方向的极坐标;左下:三体系统的瓦解时标;中下:双星系统的轨道半长轴;右下:双星系统的偏心率。(图片来源:Boekholt & Portegies Zwart 2014)
在宏观性质方面,作者还考察了两种算法给出的逃逸天体的身份。对于瓦解时标足够短的系统来说,当逃逸天体出现时,各种计算误差还没有来得及积累起来,因此两种算法结果相同。反之,Brutus与Hermite算法之间出现了“交换”现象,也就是对于同样的初始条件和系统构型,最终逃逸的却是不同的天体。三体质量相等的冷系统两种算法出现交换的概率最大,可以达到6成,而质量不等的系统交换的概率大大减小,较前者降低了一半左右。这一条在直观上也很好懂,因为在质量不等的系统中,质量最大的天体在引力上占据了支配地位,而较轻的天体更容易受到扰动并逃逸出去;等质量系统就要麻烦很多了,很可能在位置或速度上的一点点小偏差就会带来截然不同的结果。
因此这项工作的结论就是,可靠的真实收敛解(Brutus)可以在统计学上用近似解(Hermite算法)来模拟,但对于具体系统来说则不可以,大致说来,Hermite算法只有大约一半的结果是可以信赖的,因此本文开头提到的假设得以验证。但这里必须特别指明的是,出于节约时间的考虑,作者模拟的过程时标都不是很长,因此系统长期演化过程中两种算法是否会出现新的偏差还不得而知,尚待今后的进一步研究。