[转载] 从Ramsey理论到Green-Tao定理的史话
[2] Pell方程的连分数解法
“研究算术给我带来很多困难,也许是最不划算的。”——Lagrange (拉格朗日)
前面说过Archimedes牛群问题直到1773年才被重新发现。 1657年Fermat公开指出,正整数d不是完全平方时方程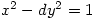 有无穷多组整数解;与他的其它断言一样,Fermat本人没有对此提供证明细节。即使对于较小的d, 对应Pell方程的最小正整数解也可能很大;例如:
有无穷多组整数解;与他的其它断言一样,Fermat本人没有对此提供证明细节。即使对于较小的d, 对应Pell方程的最小正整数解也可能很大;例如: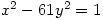 的最小正整数解为x=1766319049, y=226153980。由此可见Archimedes与Fermat的断言是多么大胆与深刻!
的最小正整数解为x=1766319049, y=226153980。由此可见Archimedes与Fermat的断言是多么大胆与深刻!
法国数学家Fermat (1601-1665)可谓“业余数学家之王”,其正式职业为法官或律师。他求极值的方法启示Newton(1643-1727)发明了微积分,他与Pascal(1623-1662)对赌博问题的通信讨论开创了概率论,他在丢番图著作拉丁译本上所作的注记中提出了困惑后人长达358年之久的Fermat大定理(对每个n=3,4,…方程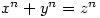 无正整数解)。Fermat是数论的奠基人,他陈述了基本又重要的Fermat小定理(对于素数p与整数a,
无正整数解)。Fermat是数论的奠基人,他陈述了基本又重要的Fermat小定理(对于素数p与整数a, 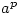 与a相差一个p的倍数), 指出奇素数p可表成两个整数的平方和当且仅当p被4除余1, 断言每个自然数是k个k角数之和(三角数形如x(x+1)/2, 平方数是四角数),还探讨Fermat数
与a相差一个p的倍数), 指出奇素数p可表成两个整数的平方和当且仅当p被4除余1, 断言每个自然数是k个k角数之和(三角数形如x(x+1)/2, 平方数是四角数),还探讨Fermat数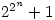 中的素数(后来Gauss证明正m边形可用圆规与直尺作出当且仅当m是2的幂次(包括1)与不同Fermat素数的乘积),……。这一切充分展示了Fermat远超常人的直觉与令人敬畏的才能。
中的素数(后来Gauss证明正m边形可用圆规与直尺作出当且仅当m是2的幂次(包括1)与不同Fermat素数的乘积),……。这一切充分展示了Fermat远超常人的直觉与令人敬畏的才能。
数论之父Fermat提出Pell方程问题后Brouncker指出了解这种方程的系统方法,完备的解答与详细的讨论则由Lagrange在1766年用连分数给出。Pell方程的名称是大数学家Euler给的,其实Pell只是在他1668年编辑的书中收入了Brouncker的方法。既然数学大师Euler这么称呼,大家也就将错就错沿用着Pell方程这个错误的命名。(知错不改的例子还有“心想事成”;古人认为心脏有思想,后来发现只有大脑会思考。)
瑞士数学家Euler (1707-1783) 是18世纪数学巨星,迄今为止最高产的科学家。尽管他在29岁时右眼失明,59岁时左眼失明,Euler全集仍有72卷之多!Euler勤奋一生,在微积分、数论、力学等许多领域有着卓越的贡献;数学界公认Euler为“数学家之英雄”,数学上以Euler命名的东西很多,例如:Euler函数(来自他对Fermat小定理的推广),Euler常数,Euler方程,Euler定理,…在数论上Euler认真研究Fermat的断言,证明了Fermat所说的4倍数加1的素数可唯一表成两个正整数的平方和等等。法国数学家Lagrange(1736-1813)在19岁时就作出了变分法的伟大发现,并开始与Euler通信。尽管Lagrange终生未与Euler见过面而且与之关系总的比较冷淡,但他的大部分工作与Euler有关又不乏创造性,例如:在Euler多年工作的基础上他完成了证明每个自然数是四个整数平方和的最后一步。顺便说一句,Euler与Lagrange都经历了两次婚姻;前者有13个子女,而后者没有孩子。
下面介绍一下连分数知识以及Lagrange对Pell方程的解法。
对于整数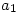 及非零整数
及非零整数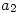 ,
,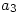 ,……
,……
![[a_1,a_2]=a_1+1/{a_2 [a_1,a_2]=a_1+1/{a_2](/website/wp-content/plugins/pictures/b303b7a1495f3edf750a66e3788862c8.gif) ,
,
![[a_1,a_2,a_3]=a_1+1/(a_2+1/a_3) [a_1,a_2,a_3]=a_1+1/(a_2+1/a_3)](/website/wp-content/plugins/pictures/fbb9154dfc86b4b091d455562dea4db7.gif) ,
,
![[a_1,a_2,a_3,a_4]=a_1+1/(a_2+1/(a_3+1/a_4)) [a_1,a_2,a_3,a_4]=a_1+1/(a_2+1/(a_3+1/a_4))](/website/wp-content/plugins/pictures/aba97b36d84ad10dbee9c7f6717f329f.gif) , ……
, ……
都叫简单连分数。有理数可表成有限简单连分数[这实际上对应于求分子与分母最大公因数的Euclid(约公元前330-275)辗转相除法],例如:
157/68=2+21/68=2+1/(3+5/21)=2+1/(3+1/(4+1/5))=[2,3,4,5]
可以证明任何无理数可唯一地表成无限简单连分数。让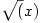 表示x>0的平方根。由于
表示x>0的平方根。由于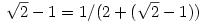 且
且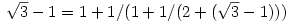 , 我们可得
, 我们可得![\sqrt{2}[1,2,,2,…] \sqrt{2}[1,2,,2,…]](/website/wp-content/plugins/pictures/3895ad9fe992818d21cfafd95a5642a4.gif) 与
与![\sqrt{3}=[1,1,2,1,2,1,2,…] \sqrt{3}=[1,1,2,1,2,1,2,…]](/website/wp-content/plugins/pictures/5d60c36d389011d15a456a9ce1d9c9ea.gif) 。
。
著名的Fibonacci(约1170-1250)数列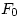 ,
, 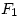 ,
,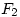 ,……如下递归地定义:
,……如下递归地定义:
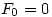 ,
,
 ,
,
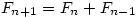
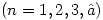
由于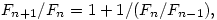 易证F_{n+1}/F_n在n趋于无穷时的极限x适合方程x=1+1/x, 解得正根
易证F_{n+1}/F_n在n趋于无穷时的极限x适合方程x=1+1/x, 解得正根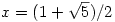 ,如此得到
,如此得到![(1+\sqrt{5})/2=[1,1,1,…] (1+\sqrt{5})/2=[1,1,1,…]](/website/wp-content/plugins/pictures/b19e97952a60a20f3e5918d6453f93b4.gif) 。 有理数的十进制展式是循环的,但
。 有理数的十进制展式是循环的,但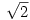 ,
,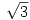 ,
,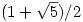 的十进制展开式毫无规律,这表明连分数的确是研究无理数的合适工具!
的十进制展开式毫无规律,这表明连分数的确是研究无理数的合适工具!
Lagrange定理:一个无理数可用循环简单连分数表示当且仅当它是二次代数数(即某个
整系数二次方程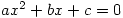 的根)。
的根)。
对于不是平方数的正整数d, [Unparseable or potentially dangerous latex formula. Error 4 ]循环简单连分数表示形如![[a_1,a_2,…,a_n,2a_1,a_2,…,a_n,2a_1,a_2,…,a_n,2a_1,…] [a_1,a_2,…,a_n,2a_1,a_2,…,a_n,2a_1,a_2,…,a_n,2a_1,…]](/website/wp-content/plugins/pictures/b7f4c204899792be8ff28de5de9ee8a0.gif) ,而且还有
,而且还有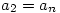 ,
,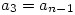 ,……设[Unparseable or potentially dangerous latex formula. Error 4 ],(其中
,……设[Unparseable or potentially dangerous latex formula. Error 4 ],(其中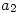 ,…,
,…,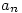 那一段重复了k次)的分子、分母分别为是
那一段重复了k次)的分子、分母分别为是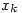 与
与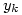 ,则可证
,则可证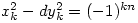 。
。
因此,通过让k取1,2,3,..(当n为偶数时)或2,4,6,…(当n为奇数时),我们可得到Pell方程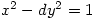 的无穷多组正整数解。例如:
的无穷多组正整数解。例如:
[Unparseable or potentially dangerous latex formula. Error 4 ],故 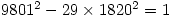 。
。
圆周率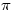 与数e也有有趣的连分数展式。 例如:
与数e也有有趣的连分数展式。 例如:
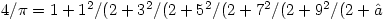 (Brouncker, 1658)
(Brouncker, 1658)
![e-1=[1,1,2,1,1,4,1,1,6,1,1,8,…] e-1=[1,1,2,1,1,4,1,1,6,1,1,8,…]](/website/wp-content/plugins/pictures/5d756ccceac2f93356487baf403cbe5f.gif) (Euler, 1737)
(Euler, 1737)
再说说与Lagrange定理有关的一段往事吧。1986年的一个晚上,南大学生科协在大学生俱乐部主办了一场歌舞晚会,期间有一位老外前往欣赏。我那在科协的老兄把我叫去跟他英语会话,一了解才知道他是叶彦谦教授请来的微分方程专家Martinet教授,这是我认识的第一位外国数学家。当听我说对数论有兴趣时,这位法国数学家说他也对数论很着迷,并经常邀我去他那儿聊数论。他还给我展示他对上述Lagrange定理的新证明,这几页纸头我一直珍藏多年。他回国后经常给我寄些我所研究课题方面的资料,这对还是学生的我无疑是雪中送炭!几年前我得悉Martinet教授因肝癌去世深感悲痛。我对他一直充满感激,我发表于国外的第一篇论文(90年)中对他作了致谢;为写那篇论文,在计算机系的高中同学用50张复印卷换来50张A4白纸提供给还是穷学生的我,那时的条件艰苦啊。
下次我们从代数的观点来看Pell方程。